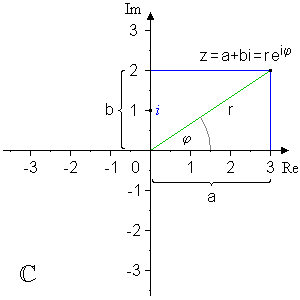
Am Montag und Mittwoch der Wissenschaftswoche um 10 Uhr nahmen Schüler der Mathematik- und Informatikkurse aus Klasse 11 und 13 an einer Vorlesung über komplexe Zahlen an der Uni Potsdam teil. Daran schloss sich eine Übung an, wie sie auch im normalen Vorlesungsbetrieb abgehalten wird. Als Dozent konnte Dr. Brückner vom Lehrstuhl Didaktik der Mathematik gewonnen werden.

Heranführung an komplexe Zahlen
In der Sekundarstufe I wird vorrangig mit rationalen Zahlen gerechnet. Bestimmte Umformungen führen allerdings schnell aus diesem Zahlbereich heraus. Zum Beispiel liegt die Wurzel aus 2 nicht mehr im Bereich Q, wohl aber im größeren Zahlbereich der reellen Zahlen R.
Analog verhält es sich mit der Wurzel aus -1. Im Bereich der reellen Zahlen ist die Gleichung x² = -1 nicht lösbar. Im Bereich der komplexen Zahlen C dagegen wird die imaginäre Einheit i = √-1 eingeführt. Damit existieren für diese quadratische Gleichung genau zwei komplexe Lösungen: i und -i. Die Probe bestätigt:
i² = -1 und (-i)² = i² = -1.

Wie kann man sich eine komplexe Zahl vorstellen?   

Allgemein besitzt eine komplexe Zahl z die Form z = a + bi. Hierbei heißt a Realteil (Re) und b Imaginärteil (Im) der komplexen Zahl. Zum Beispiel ist für z = 3 + 2i der Realteil 3 und der Imaginärteil 2. Die beiden Bestandteile der komplexen Zahl können in der Zahlenebene von Gauß dargestellt werden. Es handelt sich dabei um ein gewöhnliches Koordinatensystem mit anderen Achsenbezeichnungen.

Insgesamt haben wir also endlich die Möglichkeit, aus negativen Zahlen die Wurzel zu ziehen. Das hat unter anderem folgende angenehme Konsequenz: Eine ganzrationale Funktion n-ten Grades hat im Bereich der komplexen Zahlen immer genau n Nullstellen. Nehmen wir z.B. die Funktion f(x) = x⁴ - 81. Im Bereich der reellen Zahlen mussten wir uns mit den Nullstellen x₁ = 3 und x₂ = -3 begnügen. Im Bereich der komplexen Zahlen kommen noch die „vermissten“ zwei Nullstellen hinzu: x₃ = 3i und x₄ = -3i.

Nimmt man die Darstellung der komplexen Zahlen im Koordinatensystem, so fällt auf, dass eine komplexe Zahl durch ihre Länge r und ihren Winkel φ mit der x-Achse festgelegt ist. Hieraus ergibt sich eine andere, oft nützliche Darstellungsform für komplexe Zahlen, die Exponentialform: z = re^iφ.

Mit komplexen Zahlen kann man genauso rechnen, wie mit reellen Zahlen, ...

... solange man i² = -1 beachtet